2024.05.12_学习日记

天气：晴
学习地点：宿舍
学习时长：10h

学习内容

1. 一维牛顿法
   
   
   一维牛顿法的基本思想是用迭代点的梯度信息和二阶导数对目标函数进行二次函数逼近，然后把二次函数的极小值作为新的迭代点，并不断重复这一过程，直到求出极小点。
   牛顿法的好处在于收敛速度快，缺点在于计算二阶导数的计算量大以及求解线性方程组确定搜索方向可能是病态的。
2. 割线法
   
   在牛顿法中，每一步都需要计算当前点的导数值，需要手动求导。如果不想人工求导，可以使用两点割线来代替切线，从而得到割线法，因此割线法又称分立牛顿法。这时候当前位置的值需要上一个和上上个一阶导数的信息。
3. 非精确一维搜索——armijo条件：步长可能会很短
   
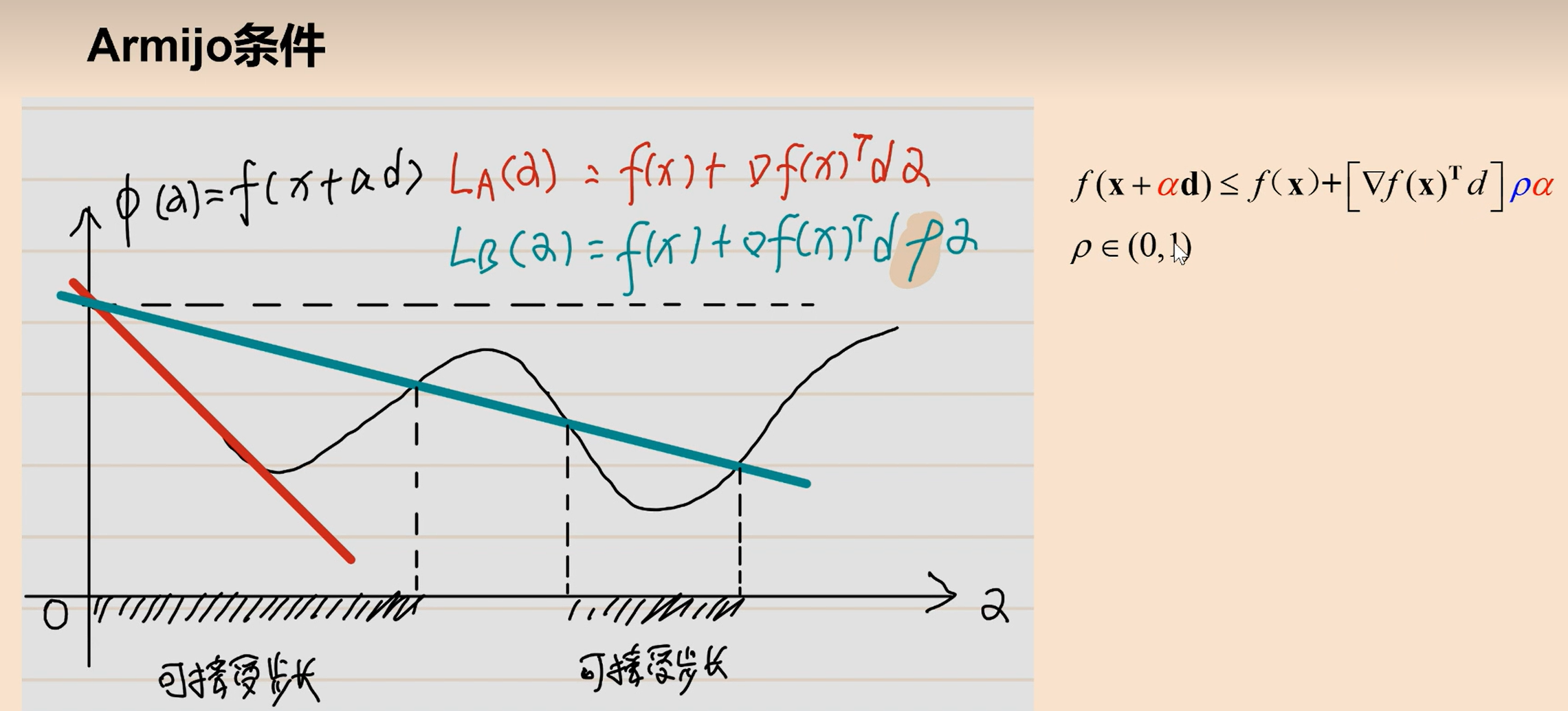
   goldstein条件：让步长不短也不长（用的不多）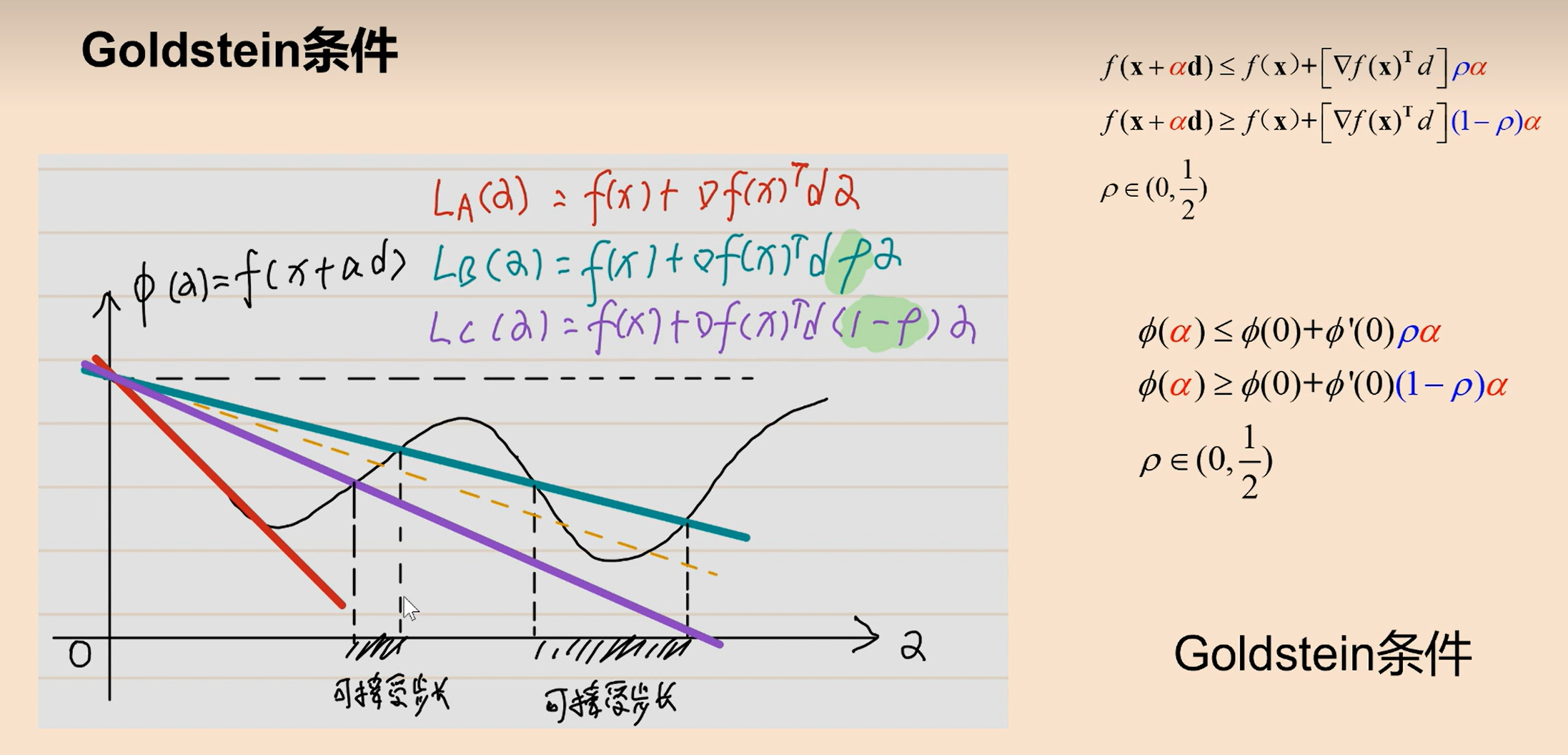
   
   缺点是条件会限制的很死。
   wolfe和强wolfe条件（用的多）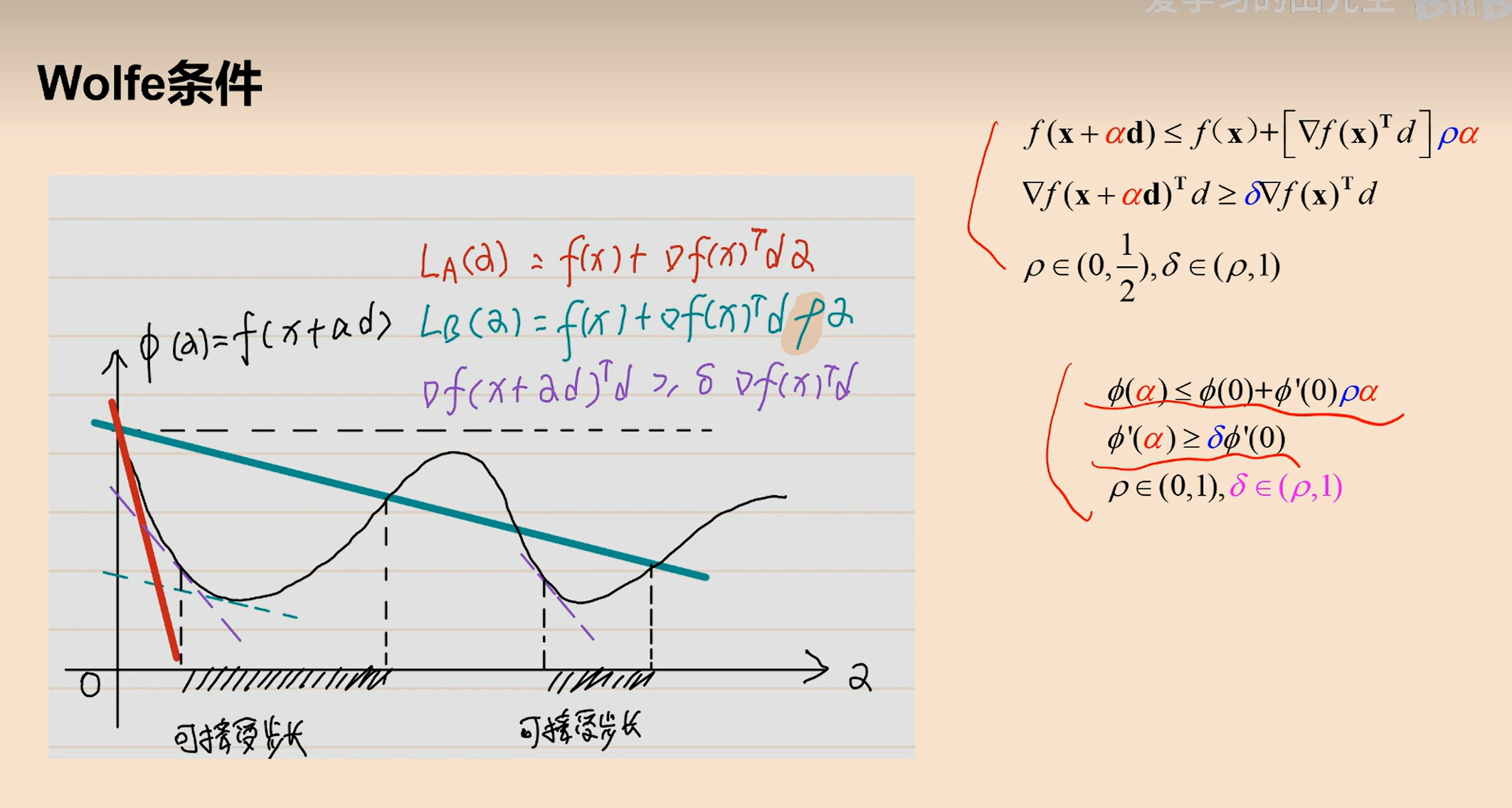
   
   在armijo条件下方，在梯度方向上方。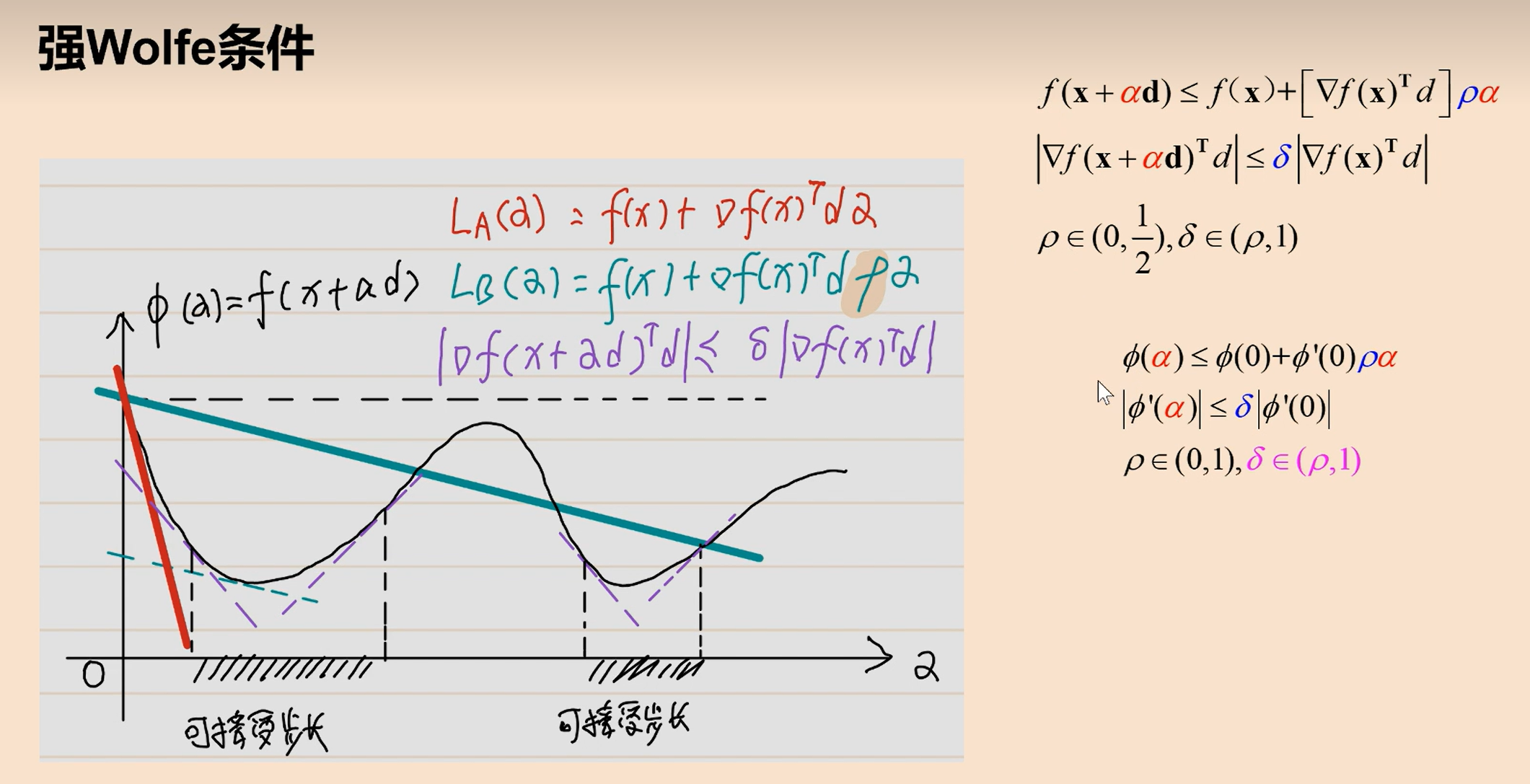
   
   左边和右边都构建一个势。
   回溯法：适合armijo条件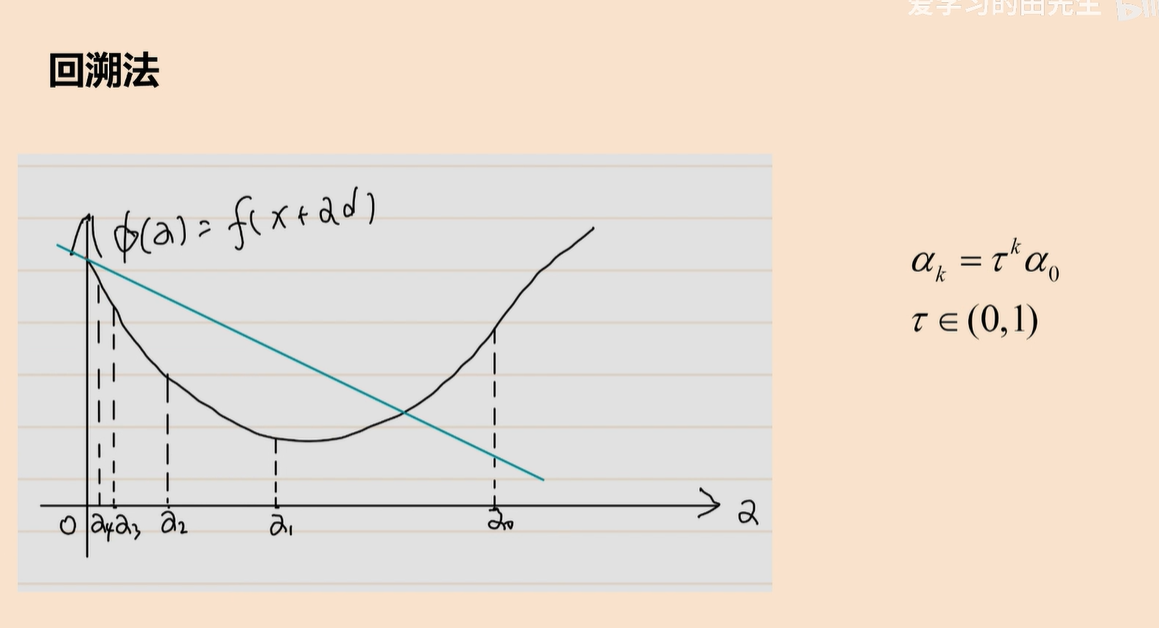
   
   先选一个a0，然后乘一个数，看是不是在armijo条件内。
   内插法：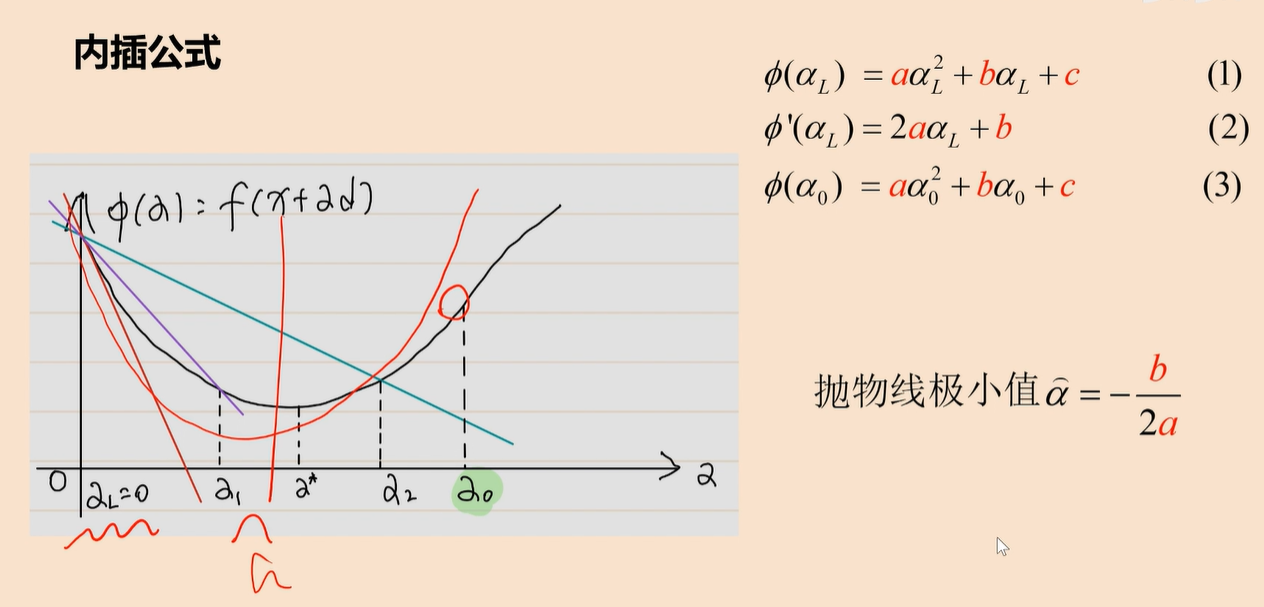
   
   把a0点和y轴的点求解抛物线方程，然后找到对称轴点继续迭代。这两个点在对称轴两边。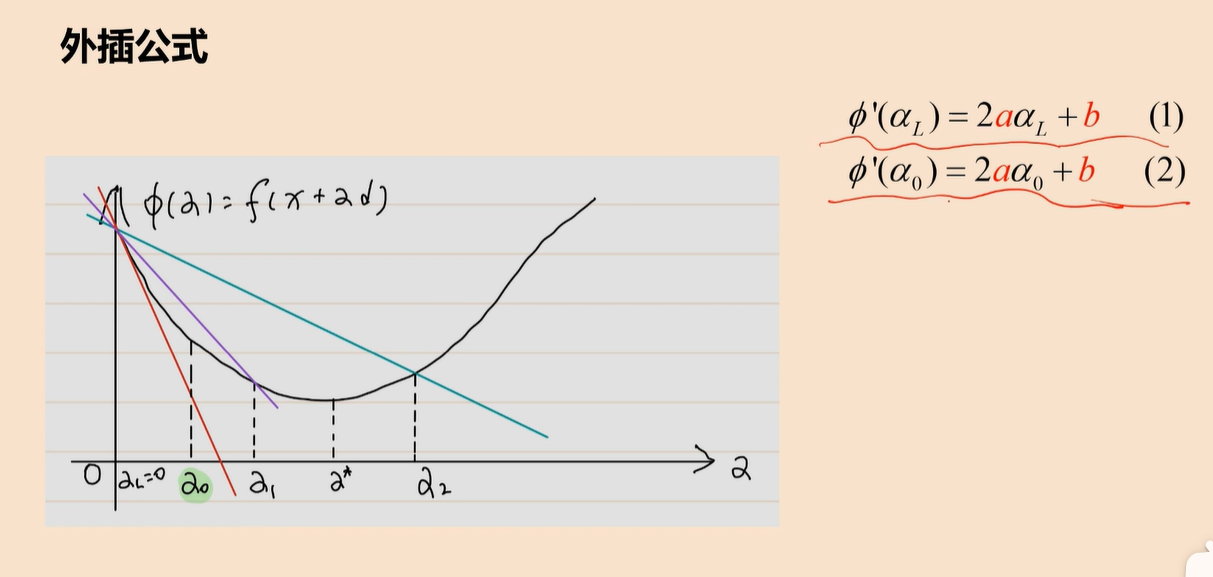
   
   外插法是利用两个点的导数性质求对称轴点，因为两个点在对称轴同一边。
4. 二分法
   
5. 最速下降法
   
   缺点：需要指出的是，某点的负梯度方向，通常只是在该点附近才具有这种最速下降的性质。
   在一般情况下，当用最速下降法寻找极小点时，其搜索路径呈直角锯齿状（如下图），在开头 几步，目标函数下降较快；但在接近极小点时，收敛速度长久不理想了。特别适当目标函数的等值 线为比较扁平的椭圆时，收敛就更慢了。实用中常用最速下降法和其他方法联合应用，在前期使用最速下降法，而在接近极小值点时，可改用收敛较快的其他方法。
6. 多维牛顿法
   
   黑塞矩阵可能是奇异矩阵，不能求逆。黑塞矩阵非正定。
   如何保持下降特性，可以优化寻找步长，找到合适的步长使得保持下降特性。
   如何让非正定矩阵变成正定，那就让黑塞矩阵加一个对角矩阵，让其正定。
   
7. 高斯模糊
   一种数据平滑技术（data smoothing），适用于多个场合。所谓”模糊”，可以理解成每一个像素都取周边像素的平均值。既然每个点都要取周边像素的平均值，那么应该如何分配权重呢？如果使用简单平均，显然不是很合理，因为图像都是连续的，越靠近的点关系越密切，越远离的点关系越疏远。因此，加权平均更合理，距离越近的点权重越大，距离越远的点权重越小。正态分布是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。先在水平方向上做一维卷积，再在垂直方向上做一维卷积，二维高斯卷积操作得以拆分。
8. 数值计算

矩阵三角分解法：

LU分解：第一行一样

TM分解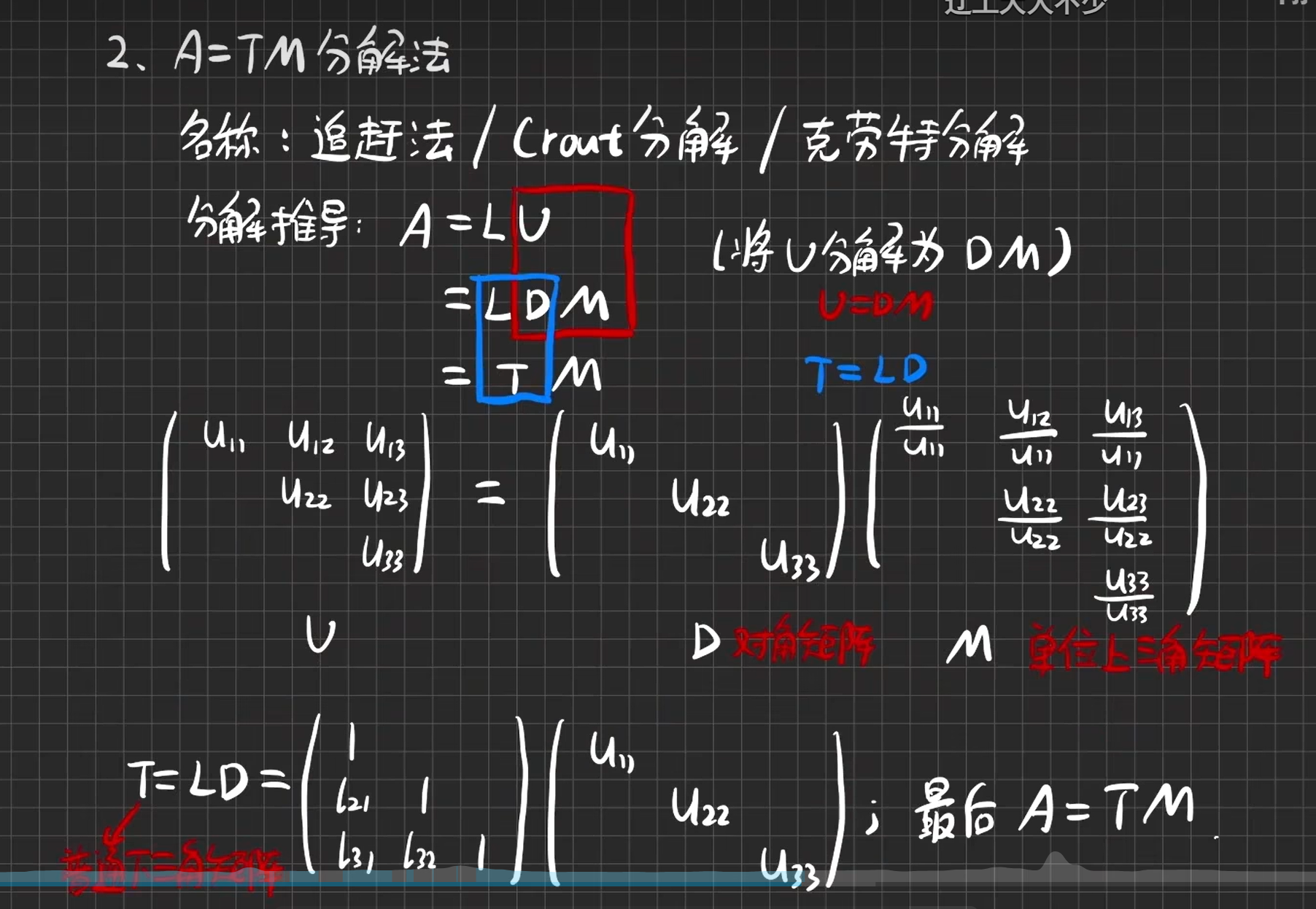


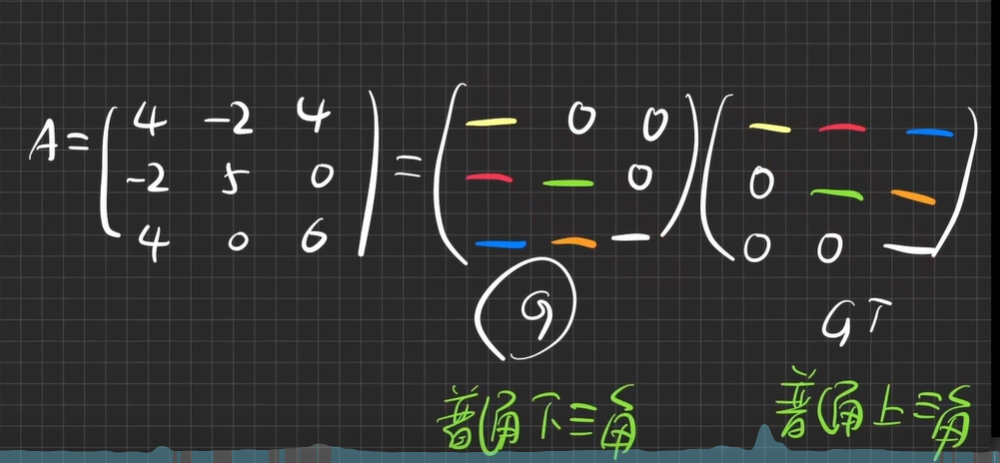
GG分解

拉格朗日插值多项式：


差商（牛顿插值法）：