2024.05.07_学习日记
天气:中雨
学习地点:宿舍
学习时长:10h
学习内容
- 算法题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
# 如果字符串为空,返回0
if len(s) == 0:
return 0
# 创建一个哈希表来存储字符及其索引
hashmap = {}
# 初始化哈希表,将字符串的第一个字符加入其中
hashmap[s[0]] = 0
# 获取输入字符串的长度
n = len(s)
# 将答案初始化为1,因为至少有一个字符
ans = 1
# 初始化变量 'pre',用于跟踪到当前字符为止的子字符串长度
pre = 1
# 从第二个字符开始遍历字符串中的字符
for i in range(1, n):
# 如果当前字符已经在哈希表中
if s[i] in hashmap:
# 计算当前索引 'i' 与该字符上次出现的索引之间的距离
p1 = i - hashmap[s[i]]
else:
# 如果当前字符不在哈希表中,距离就是当前索引加1(表示当前字符与前面的字符都不相同)
p1 = i + 1
# 计算当前字符与前一个字符不重复的子字符串的长度
p2 = pre + 1
cur = min(p1, p2)
# 更新答案为当前子字符串长度与之前的答案中的较大值
ans = max(ans, cur)
# 更新变量 'pre' 为当前子字符串的长度,以备下一轮迭代使用
pre = cur
# 更新哈希表中当前字符的索引
hashmap[s[i]] = i
# 返回最终答案
return ans - lc困难题
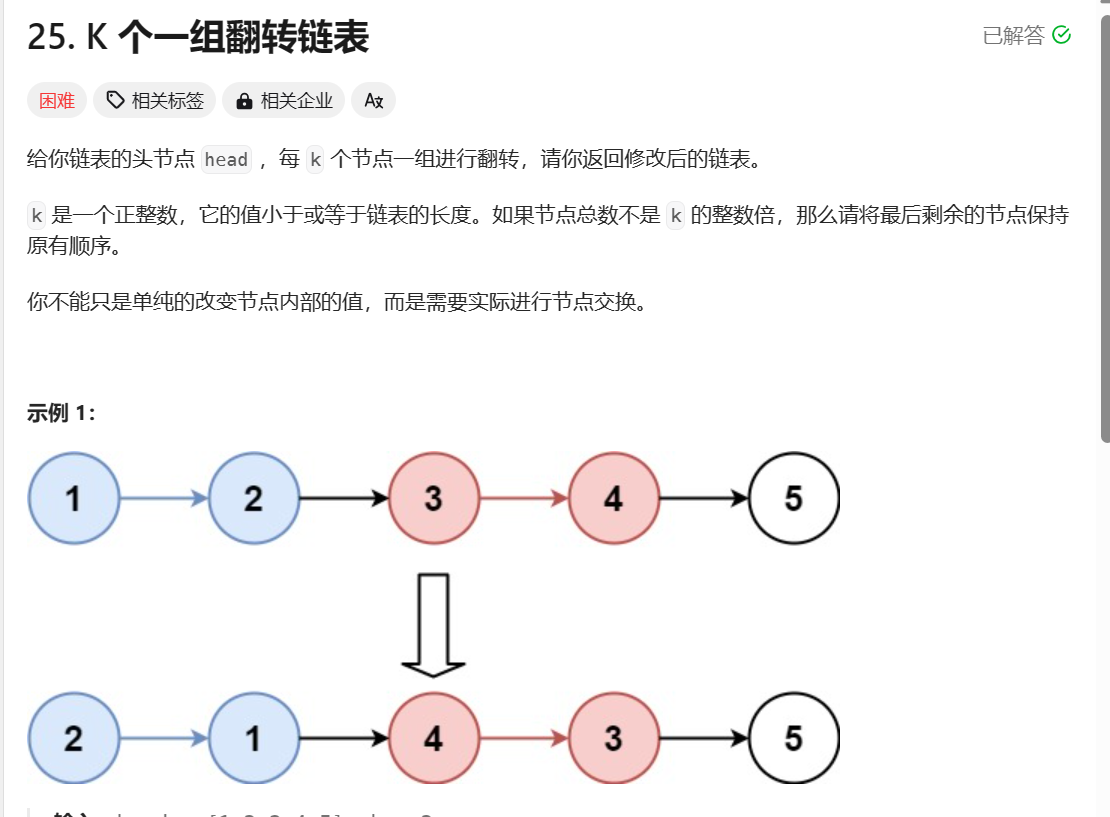
这个题最后一定要把head=cur并且返回head,而不能省略这一步返回cur,因为这才能让最后没有k长度的结点的部分连上去。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
# 初始化当前节点为头结点
cur = head
# 计数器,用于记录当前已经遍历的节点个数
cnt = 0
# 遍历链表,直到当前节点为空或已经遍历了k个节点
while cur and cnt != k:
# 移动到下一个节点
cur = cur.next
# 增加计数器
cnt += 1
# 如果已经遍历了k个节点
if cnt == k:
# 递归调用reverseKGroup函数,对剩余节点进行分组翻转
cur = self.reverseKGroup(cur, k)
# 当前组翻转完成后,将当前组的节点进行翻转
while cnt:
# 减少计数器
cnt -= 1
# 临时保存头结点的下一个节点
tmp = head.next
# 将头结点的next指针指向已经翻转好的剩余节点
head.next = cur
# 更新cur为头结点,以便下一轮循环
cur = head
# 更新头结点为下一个节点,继续遍历
head = tmp
# 更新头结点为翻转后的头结点
head = cur
# 返回翻转后的头结点
return head - 算法题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
def process(nums, k):
# 随机选择一个元素作为枢轴
pivot = nums[random.randint(0, len(nums)-1)]
# 初始化三个列表,用于存放比枢轴大、小和相等的元素
big, small, equal = [], [], []
# 遍历数组,根据与枢轴的大小关系将元素放入对应的列表中
for num in nums:
if num < pivot:
small.append(num)
elif num > pivot:
big.append(num)
else:
equal.append(num)
# 如果要找的第 k 大的元素在大于枢轴的列表中
if k <= len(big):
# 递归处理大于枢轴的列表
return process(big, k)
# 如果要找的第 k 大的元素在小于枢轴的列表中
if len(nums) - len(small) < k:
# 递归处理小于枢轴的列表,并调整第 k 的值
return process(small, k-(len(nums)-len(small)))
else:
# 如果第 k 大的元素正好等于枢轴,则返回枢轴
return pivot
# 调用递归函数,并返回结果
return process(nums, k) - 二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution:
def search(self, nums: List[int], target: int) -> int:
# 初始化左右边界
l, r = 0, len(nums)-1
# 开始二分查找
while l <= r:
# 计算中间位置
mid = (l+r) // 2
# 如果中间位置的元素就是目标值,返回该位置
if nums[mid] == target:
return mid
# 如果中间位置的元素大于等于左边界的元素,说明左半部分是有序的
if nums[0] <= nums[mid]:
# 如果目标值在左半部分且不大于中间位置的元素,将搜索范围缩小为左半部分
if nums[l] <= target < nums[mid]:
r = mid - 1
else:
# 否则,将搜索范围缩小为右半部分
l = mid + 1
else:
# 如果中间位置的元素小于左边界的元素,说明左半部分不是有序的,右半部分是有序的
# 如果目标值在右半部分且不小于中间位置的元素,将搜索范围缩小为右半部分
if nums[mid] < target <= nums[r]:
l = mid + 1
else:
# 否则,将搜索范围缩小为左半部分
r = mid - 1
# 如果没有找到目标值,返回-1
return -1