2024.04.22_学习日记
天气:晴
学习地点:图书馆
学习时长:10h
学习内容
- 二叉树树形dp问题(图)
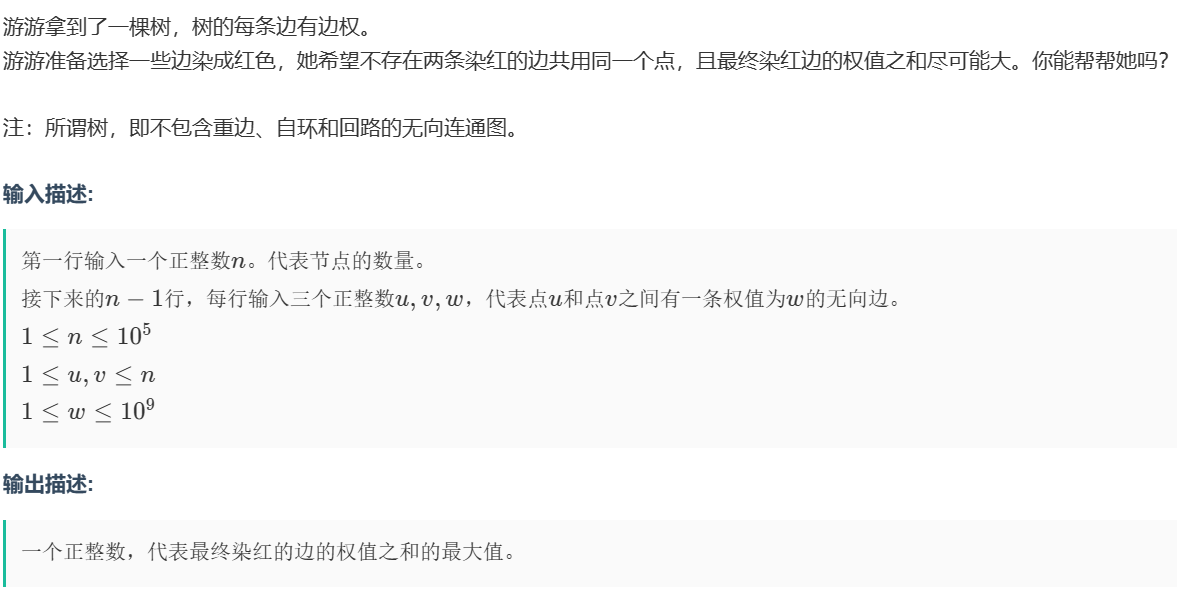
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43def solve(cur, pre, s):
# 如果当前节点的状态已经计算过,则直接返回结果
if dp[cur][s] != -1:
return dp[cur][s]
notch = 0 # 记录不选当前节点时的最大价值
# 遍历当前节点的邻居节点
for nx, w in nxt[cur]:
if nx != pre: # 如果邻居节点不是当前节点的父节点
# 递归计算不选当前邻居节点时的最大价值,并累加到 notch 中
notch += solve(nx, cur, 1)
# 如果当前节点的状态为不选,则直接返回 notch
if s == 0:
return notch
ch = 0 # 记录当前节点选择时的最大价值
# 遍历当前节点的邻居节点
for i in range(len(nxt[cur])):
tmp = 0
for j in range(len(nxt[cur])):
nx, w = nxt[cur][j]
if nx != pre: # 如果邻居节点不是当前节点的父节点
if j == i: # 如果当前邻居节点是第 i 个
# 选择当前邻居节点,并递归计算其不选时的最大价值,累加到 tmp 中,并加上权值 w
tmp += solve(nx, cur, 0) + w
else:
# 不选择当前邻居节点,并递归计算其最大价值,累加到 tmp 中
tmp += solve(nx, cur, 1)
# 更新当前节点选择时的最大价值
ch = max(ch,tmp)
# 更新动态规划数组中当前节点的状态值为当前节点选择和不选择的最大价值
dp[cur][s] = max(ch, notch)
return dp[cur][s]
if __name__ == '__main__':
n = int(input()) # 输入节点数量 n
nxt = {i:[] for i in range(1, n+1)} # 初始化邻接表,键值从1开始
for i in range(n-1):
u, v, w = map(int, input().split()) # 输入每条边的起点、终点和权值
nxt[u].append((v,w)) # 将边加入邻接表
nxt[v].append((u,w)) # 因为是无向图,所以边需要双向加入
dp = [[-1,-1] for _ in range(n+1)] # 初始化动态规划数组
# 调用 solve 函数计算根节点选择时的最大价值,并打印结果
res = solve(1,-1,1)
print(res) - 数组题

1
2
3
4
5
6
7
8
9
10
11
12
13
14# 读取测试用例数量 t
t = int(input())
# 遍历每个测试用例
for _ in range(t):
# 读取整数 a 和字符串 b
a, b = input().split()
a = int(a) # 将字符串转换为整数
bb = int(b) # 将字符串转换为整数(这里存在错误,应该是 int(b) 而非 bb)
res = 0 # 初始化结果变量为 0
# 遍历字符串 b 中的每个字符
for i in range(len(b)):
res += int(b[i]) * a # 将每个字符转换为整数并与 a 相乘,然后累加到结果中
# 输出结果
print(res) - 算法题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20# 读取输入的两个字符串 s 和 t
s = input()
t = input()
# 获取字符串 s 和 t 的长度
n = len(s)
m = len(t)
# 将字符串 s 扩展一倍,以便处理循环匹配的情况
s += s[0:n-1]
# 初始化计数器 res 为 0
res = 0
# 遍历字符串 s 中的每个字符
for i in range(n):
# 如果当前字符与 t 的首字符不匹配,跳过当前循环
if s[i] != t[0]:
continue
# 如果 s 中从当前位置开始长度为 m 的子串与 t 完全匹配,计数器 res 加 1
if s[i:i+m] == t:
res += 1
# 输出匹配次数
print(res) - 动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13n = int(input()) # 输入操作次数
a = list(map(int, input().split())) # 输入每个数字的得分
s = input() # 输入数字的颜色标记
f = [0] * (n) # 创建长度为 n 的数组 f,用于记录每个位置的最大得分
# 开始遍历数字标记 s,从第二个数字开始(下标为 1),直到最后一个数字
for i in range(1, n):
f[i] = f[i - 1] # 将当前位置的得分设置为上一个位置的得分
# 检查当前数字的颜色标记与前一个数字的颜色标记是否相同
if s[i] != s[i - 1]:
# 如果不同,则可以进行标记操作,更新当前位置的得分
f[i] = max(f[i], f[i - 2] + a[i] + a[i - 1])
# 输出数组 f 的最后一个元素,即小红最多能获得的分数
print(f[n - 1]) - 算法题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27# 读取操作次数
n = int(input())
# 初始化得分数组,长度为9,下标0-7对应位置得分,下标8保留
res = [0] * 9
# 循环处理每次操作
for i in range(n):
# 读取操作的角度和位置
a, b = map(int, input().split())
# 获取当前位置及相邻位置的得分
c, d, e = res[b-1:b+2]
# 根据操作角度和位置更新得分数组
if a == 0: # 操作角度为0度
x = max(c, d)
res[b-1] = x + 3
res[b] = x + 1
elif a == 90: # 操作角度为90度
x = max(c+1, d, e)
res[b-1] = res[b] = res[b+1] = x + 1
elif a == 180: # 操作角度为180度
x = max(c+1, d+3)
res[b-1] = res[b] = x
else: # 其他角度
x = max(c, d, e)
res[b-1] = res[b] = x + 1
res[b+1] = x + 2
# 输出前8个位置的得分
print(*res[0:8]) - 双指针
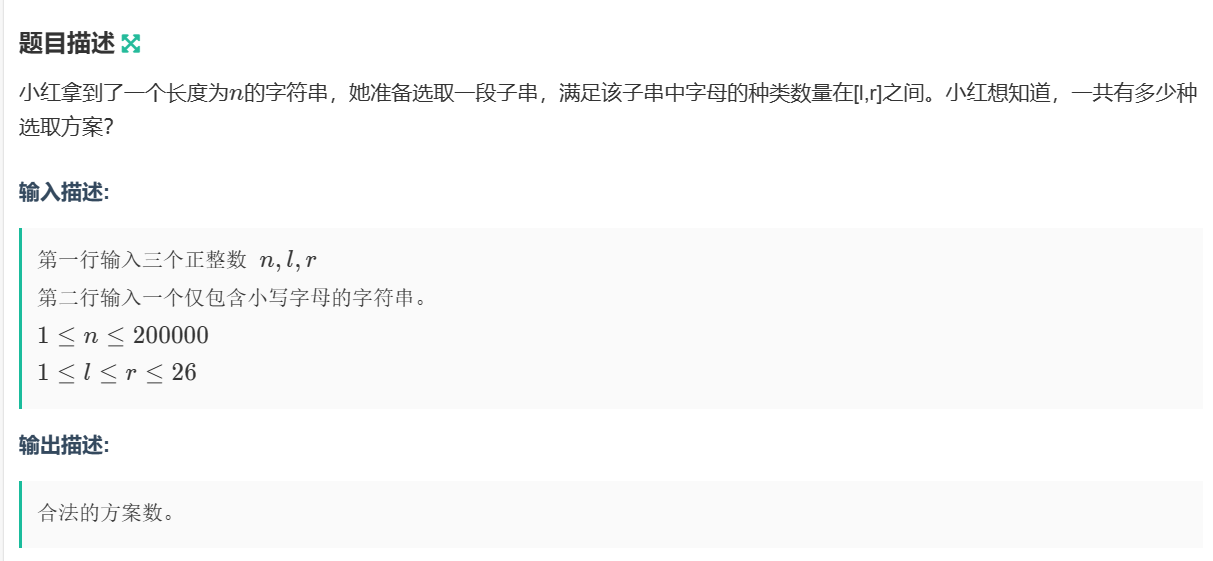
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26# 定义一个函数,计算字符种类在 [1, x] 之间的子串数量
def find(x):
if x == 0: # 如果 x 为 0,则直接返回 0
return 0
left = 0 # 左指针初始化为 0
right = 0 # 右指针初始化为 0
hash_set = [0] * 26 # 哈希集合用于记录每个字符出现的次数,初始全为 0
kinds = 0 # 字符种类数初始化为 0
ans = 0 # 结果初始化为 0
while right < n: # 右指针小于字符串长度时循环
if hash_set[ord(s[right]) - ord('a')] == 0: # 如果当前字符之前未出现过
kinds += 1 # 字符种类数加 1
hash_set[ord(s[right]) - ord('a')] += 1 # 记录当前字符出现的次数
while kinds > x: # 当字符种类数大于 x 时
if hash_set[ord(s[left]) - ord('a')] == 1: # 如果左指针所指字符只出现过一次
kinds -= 1 # 字符种类数减 1
hash_set[ord(s[left]) - ord('a')] -= 1 # 左指针右移,更新字符出现次数
left += 1 # 左指针右移
ans += right - left + 1 # 更新结果
right += 1 # 右指针右移
return ans # 返回结果
# 主函数
n, l, r = map(int, input().split()) # 读取输入,n 为字符串长度,l 和 r 为字符种类数范围
s = input() # 读取字符串
# 调用函数计算结果并输出
print(find(r) - find(l - 1)) # 计算字符种类在 [l, r] 之间的子串数量并输出 - 算法题
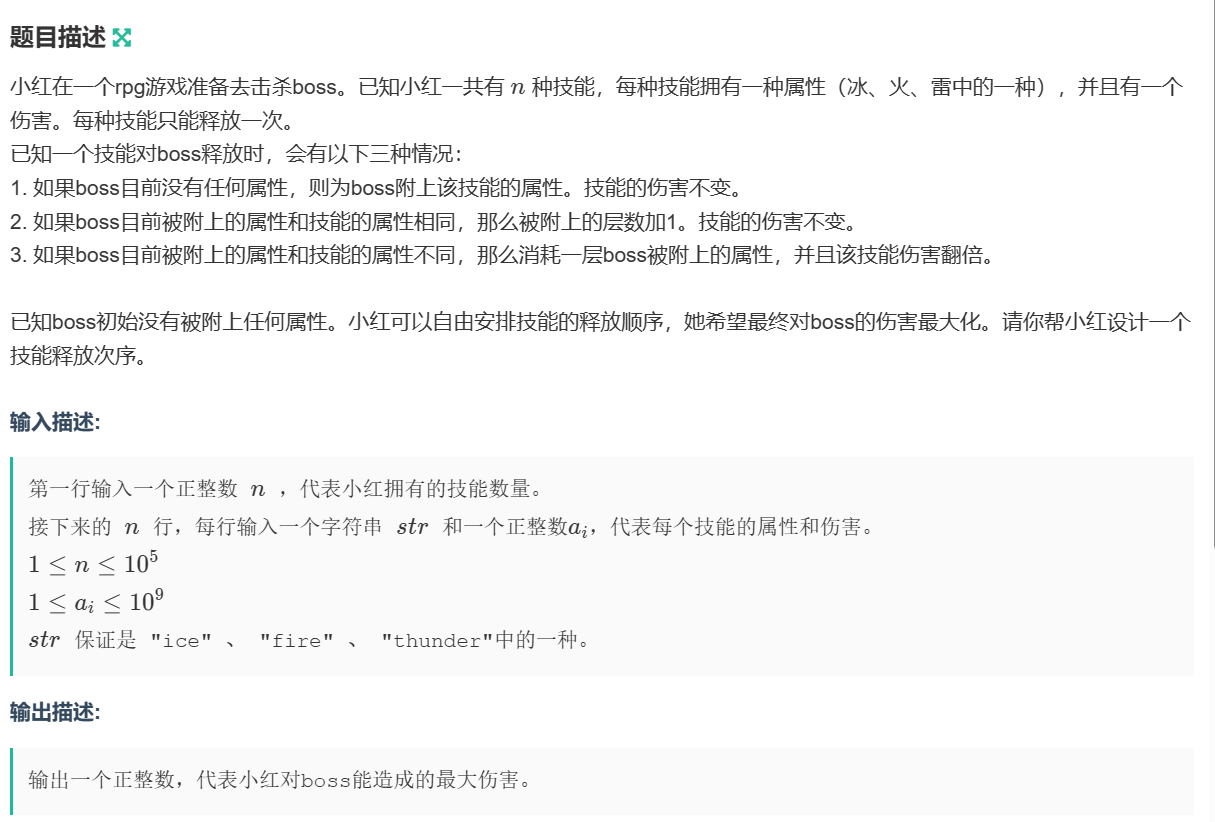
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45# 读取操作数 n
n = int(input())
# 分别用于存储不同类型的操作数的列表
a, b, c = [], [], []
# 循环读取每个操作
for _ in range(n):
op, num = input().strip().split()
num = int(num)
# 根据操作类型将操作数添加到相应的列表中
if op[0] == 'i':
a.append(num)
elif op[0] == 'f':
b.append(num)
else:
c.append(num)
# 将三个列表组成的列表按照列表长度进行排序,从小到大
arr = [a, b, c]
arr.sort(key=lambda x: len(x))
# 初始化结果变量 res
res = 0
# 分别获取排序后的列表中的三个子列表 a, b, c
a, b, c = arr
# 判断条件:如果 a 和 b 的长度之和小于等于 c 的长度
if len(a) + len(b) <= len(c):
# 计算需要剔除的 c 中的部分,并加到结果 res 中
k = len(c) - (len(a) + len(b))
c.sort()
res += sum(c[:k])
# 将 a, b, 剩余的 c 合并并排序
tmp = a + b + c[k:]
tmp.sort()
# 将列表 tmp 分成两半,并将前半部分加到结果 res 中
k = (len(tmp)+1) // 2
res += sum(tmp[:k]) + sum(tmp[k:]) * 2
else:
# 如果 a 和 b 的长度之和大于 c 的长度
# 合并三个列表并排序
tmp = a + b + c
tmp.sort()
# 计算分割位置 k
k = (n + 1) // 2
# 将列表 tmp 分成两部分,并将前半部分加到结果 res 中
res += sum(tmp[:k]) + sum(tmp[k:]) * 2
# 输出结果 res
print(res)